Sort By Grade

7ee4b

Geometry Draw, construct, and describe geometrical figures and describe the relationships between them. 1Solve problems involving scale drawings of geometric figures, including computing actual lengths and areas from a scale drawing and reproducing a scale drawing at a different scale. 1 Computations with rational numbers extend the rules for manipulating fractions to complex fractions.

7g2

List View (old)

Image Size

Smaller Larger

7g1

- finding-width-height-and-area-of-scale-rectangles worksheet

Select a Worksheet >

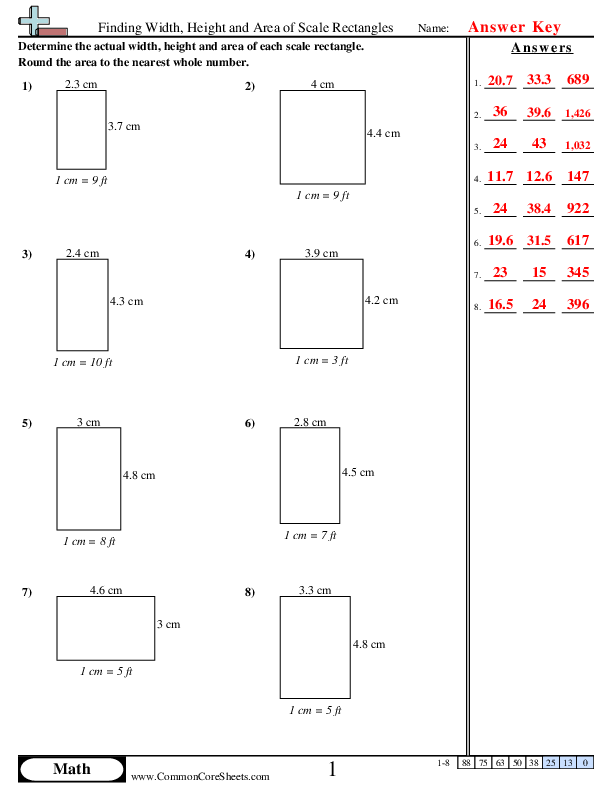
Finding Width, Height and Area of Scale Rectangles

7g1

× Description:
"This worksheet is designed for young math enthusiasts to learn about width, height, and area of scale rectangles. With 8 customizable problems, it visualizes dimension in real-life scenarios through scaled rectangular figures, measuring in centimeters and converting to feet. The lessons can be transformed into engaging flashcards or utilized in distance learning settings, making it perfect for flexible, hands-on mathematical understanding and practice."

× Student Goals:
Understanding of Mathematical ConceptsAfter going through the worksheet, students should have a profound understanding of the mathematical concepts associated with area, width, and height. They will comprehend the essence of these terms, as well as how they relate to the physical properties of shapes in our everyday lives.Problem-Solving Skills DevelopmentAchieving all tasks successfully in the worksheet means that a child has honed their problem-solving skills. Solving problems related to finding the dimensions and area of rectangles develops their ability to apply classroom learning to solve practical problems. Critical thinking and logical reasoning skills are also improved, making them better equipped to take on complex mathematical problems in the future.Awareness of Scale ConversionsThrough this worksheet, students will gain a basic understanding of units of measurement and how scales work in real-life scenarios. They cultivate an understanding of the concept of converting measurements from one scale to another, i.e., from centimeters to feet in this case. Learning this skill is crucial for real-life applications in construction, mapping, and other practical fields.Proficiency in Arithmetic CalculationsAfter completing the worksheet, a student should be proficient in performing basic arithmetic calculations like multiplication and division, key components in finding dimensions and areas of shapes. This solidifies their foundational knowledge in mathematics which paves the way for confidently tackling complex computations in the higher levels of education.Learning Through PracticeBy attempting different problems which follow a similar format, the student acquires the practical knowledge of the subject matter. As they say, practice makes perfect, hence the repetition of a certain type of problem ensures that the knowledge is embedded deeply into their understanding, hence becoming second nature to them.Mathematical Communication ImprovementThe written word is not just confined to languages. Math also has its own language. Students learn how to clearly express mathematical thinking by writing down the steps they follow in solving each problem, improving their mathematical literacy and communication.

Select a Worksheet >

Drawing Scaled Rectangles

7g1

× Description:
"This worksheet is designed to guide children in mastering the concept of scale in mathematics by drawing scaled rectangles. It contains six practical problems where students work with dimensions to create rectangles scaled up by different factors. The customizable worksheet is ideal for distance learning, and the content can also be converted into flash cards for convenient learning. It blends problem-solving with creativity, making math fun and engaging."

× Student Goals:
Understanding of Scaled DimensionsUpon completing the worksheet, students should be able to understand the concept of scaling in geometry. Specifically, they will be able to comprehend how altering one dimension of a rectangle affects the overall scale of the figure. This skill requires a clear understanding of how linear measurements interact with each other in a two-dimensional plane, which is a fundamental aspect of spatial awareness and geometric understanding.Calculation of Size IncreaseStudents will also gain proficiency in calculating size increases. They will be capable of determining how a rectangle's dimensions change when it's scaled up by a specific factor, reinforcing core multiplication skills. The problems pose real-world scenarios that students may encounter in fields that utilize geometry, such as engineering, architecture, or design.Problem Solving and Critical ThinkingBy working through these rectilinear problems, students also exercise their problem solving and critical thinking abilities. They learn to apply their math knowledge to unique settings, challenging them to think creatively and logically. These are essential skills that apply to a wide array of contexts beyond math, helping to prepare students for future academic and professional challenges.Enhanced Mathematical CommunicationAs students determine the scaled rectangles' dimensions, they are expected to communicate their understanding effectively. They can do this by accurately writing or explaining the dimensions of each rectangle. This practice helps deepen their understanding of the mathematical concept and develop their ability to explain mathematical ideas — an important component of comprehensive math literacy.Application and Transfer of SkillsFinally, students will be able to transfer and apply these skills into other areas of mathematics and their daily life. Understanding how to manipulate the sizes of shapes is not just important within the realm of geometry, but also in many practical situations such as reading maps, designing a garden, or coding a video game. Through this worksheet, students are not only able to accomplish a much deeper understanding of geometry, but develop practical life skills as well.