Algebra worksheets from common core sheets are the best on the internet! Our worksheets are designed to help students of all levels hone their algebra skills, offering a range of topics and helpful hints to provide invaluable practice in solving equations, learning new concepts, and understanding the basics of algebra. Whether you’re just starting with basic operations or tackling more complex topics like polynomials and linear equations, our algebra worksheets have you covered. Each worksheet provides an engaging way to learn and practice essential algebra skills like simplifying expressions, identifying coefficients, solving inequalities, graphing lines, and finding combinations. Get started today and take advantage of our free algebra worksheets to gain a deeper understanding of challenging concepts and experience why common core sheets is the best source for algebra worksheets available.
Browse Sheets By Problem Type
×
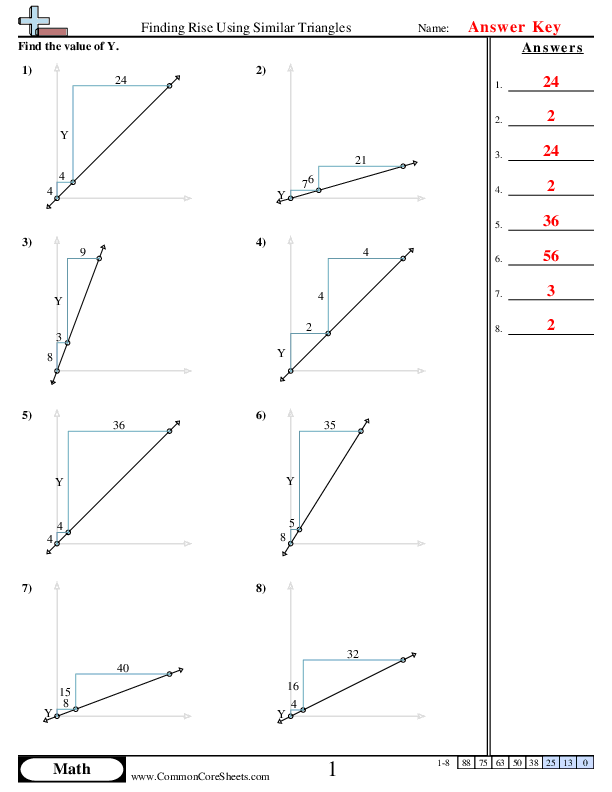
Finding Rise using Similar Triangles
8ee6


×
Description:
"This worksheet is designed to teach math students the method of finding rise using similar triangles. It involves clear, visual diagrams that encourage problem-solving and application of key mathematical concepts. With 8 interactive problems to solve, varying in complexity, students are provided with a platform to practice and understand the theory. Ideal for distance learning, these tasks can be easily converted into flash cards for revision purposes. Additionally, the worksheet is customizable, catering to specific learning styles and paces."

×
Student Goals:
Understanding of Similar TrianglesAfter completing this worksheet, students should be able to understand the concept of similar triangles effectively. They will be able to grasp how ratios and proportions can be applied in the realm of geometry, especially where triangles of identical angles but differing sizes are concerned. The students will recognize that the sides of similar triangles are proportional, thus enabling them to deduce missing measure when they are presented with partial information.Application of the Concept of RiseStudents will be able to apply the concept of 'rise' in mathematical problems. Rise is a critical concept in understanding geometric patterns and shapes, specifically triangles. As a result, students should be able to find the rise of various triangles using the principle of similarity. This crucial skill is applicable in various advanced mathematical problems and real-life scenarios, thereby enhancing problem-solving skills.Development of Problem-solving SkillsBy solving these problems, students will enhance their critical thinking and problem-solving skills. They will be forced to think beyond the box, analyze the given figures, and adapt strategies to fill in the missing information effectively. Over time, this process will instill in students the ability to apply mathematical principles in a broader context, enhancing their analytical skills.Understanding of Mathematical NotationThe worksheet will also help in understanding and interpreting mathematical notation accurately. It will boost the students' ability to read, comprehend, and execute based on the given notations, an important skill in mathematics.Boosting Mathematical ConfidenceBy successfully solving these problems, the students will gain confidence in their math abilities. Each problem solved will reinforce the comprehension of the concepts and instill confidence in their problem-solving capacity. This is of paramount importance for progressing in mathematics, a subject area that many students find daunting and challenging.



Identifying Point of Intersection with Equations
8ee8a


×
Description:
"This worksheet is designed to teach children the fundamental math concept of finding the point of intersection in equations. It comprises ten problems, increasing in difficulty, which aid in understanding how different equations intersect at a particular point. The format of the worksheet is simple yet engaging, making it suitable for conversion into customizable flashcards or even for incorporation into distance learning curricula."

×
Student Goals:
Understanding the Concept of Intersection PointsAfter completing this worksheet, students will have an in-depth understanding of intersection points in a pair of linear equations. They will learn how to identify common points at which two lines intersect in a Cartesian coordinate system. This foundational knowledge is crucial in further graphing and plotting studies.Identification and Computation of Equations SkillsThe worksheet is designed to improve students' skills in identifying and computing mathematical equations. They will gain the ability to manipulate equations to correctly locate points of intersection. This will enhance their proficiency in algebraic computation and manipulation by handling numerical coefficients and variables.Problem Solving AbilitiesThis worksheet serves to sharpen students' problem-solving abilities. As it challenges them with multiple linear equations, it requires them to apply keen logical and analytical thinking in determining intersection points. This nurtures their solving abilities, which is critical not only in math but also in daily life problem-solving situations.Critical Thinking and Reasoning DevelopmentBy solving these problems, participants will bolster their critical thinking skills and mathematical reasoning. The task of pinpointing the intersection demands careful consideration and planning, promoting the development of logical thought processes and careful evaluation of calculated solutions.Self-evaluationCompleting this worksheet equips students with the capacity for self-evaluation. As they monitor and assess their progress, they will gain insight into their strengths and areas for improvement. This reflection is important in honing their learning strategies and maintaining a proactive attitude in personal improvement.Preparation for Advanced StudyThis worksheet provides a crucial foundation for more advanced mathematical studies. Understanding the intersection of equations prepares students for future topics, including calculus, geometry, and more complex algebraic topics, and is also applicable in various fields of physics and data analysis in higher learning disciplines. Moreover, the thinking approach nurtured through this activity is beneficial in various disciplines such as engineering, software development, and scientific research.




